Dictionnaire populaire illustré d'histoire naturelle : comprenant la botanique, la zoologie, l'anthropologie, l'anatomie... (2e édition) / par J. Pizzetta (1880-1900-1930)

(article "Parasites")

 — C'est une des lois générales de la nature que
la vie s'entretienne aux dépens de la vie, que
l'existence des uns s'alimente par la mort des
autres, et rien ne pouvant venir de rien, il faut
bien, pour que l'organisation continue ses phases,
que ce soit aux dépens de quelque chose. La
vie est tout à la fois but et moyen, et les êtres
organisés sont nés pour se servir mutuellement
de pâture. La plante pousse plus vigoureusement
lorsque ses racines sont plongées dans un sol fer-
tilisé par des débris animaux, et l'animal à son
-tour vit soit de végétaux, soit de chair pour servir
lui-même plus tard de proie et de nourriture à
quelque autre espèce. L'animal carnassier suppose
nécessairement des animaux herbivores, comme
ceux-ci supposent des plantes. C'est une suite de
dominations, vivant les unes aux dépens des autres.
C'est un mal nécessaire, une loi fatale, sans la-
quelle le monde ne pourrait exister. Que devien-
drait la terre, si tous les germes animaux et végé-
taux se développaient librement ? Il ne resterait
bientôt plus assez de place dans l'air, dans les mers,
sur les continents, pour les innombrables descen-
dants de la population primitive, et nous verrions
toutes les plaies d'Égypte désoler à la fois la terre.
Rien de tout cela n'est heureusement à craindre.
Guidé par les instincts que la nature prévoyante a
mis en lui, chaque être travaille à conserver la
place qui lui est réservée, et il concourt à son insu
à assurer cet ordre admirable qui se manifeste
dans le monde. De là ces combats pour la vie, ces
luttes incessantes qui se livrent sur tous les points
du globe et qui sembleraient devoir finir par l'ex-
termination des races entières, si la fécondité iné-
puisable de la nature n'était là pour réparer toutes
les pertes.

 https://fr.wikipedia.org/wiki/R%C3%A9gression_lin%C3%A9aire

 

En statistiques, en économétrie et en apprentissage automatique, un modèle de régression linéaire est un modèle de régression qui cherche à établir une relation linéaire entre une variable, dite expliquée, et une ou plusieurs variables, dites explicatives.

On parle aussi de modèle linéaire ou de modèle de régression linéaire.

Parmi les modèles de régression linéaire, le plus simple est l'ajustement affine. Celui-ci consiste à rechercher la droite permettant d'expliquer le comportement d'une variable statistique y comme étant une fonction affine d'une autre variable statistique x.

En général, le modèle de régression linéaire désigne un modèle dans lequel l'espérance conditionnelle de y connaissant x est une fonction affine des paramètres. Cependant, on peut aussi considérer des modèles dans lesquels c'est la médiane conditionnelle de y connaissant x ou n'importe quel quantile de la distribution de y connaissant x qui est une fonction affine des paramètres¹.

Le modèle de régression linéaire est souvent estimé par la méthode des moindres carrés mais il existe aussi de nombreuses autres méthodes pour estimer ce modèle. On peut par exemple estimer le modèle par maximum de vraisemblance ou encore par inférence bayésienne.

Bien qu'ils soient souvent présentés ensemble, le modèle linéaire et la méthode des moindres carrés ne désignent pas la même chose. Le modèle linéaire désigne une classe de modèles qui peuvent être estimés par un grand nombre de méthodes, et la méthode des moindres carrés désigne une méthode d'estimation. Elle peut être utilisée pour estimer différents types de modèles. 

 

https://www.youtube.com/watch?v=99N2Th67oso

 

Bayesian for kids!:l

https://www.youtube.com/watch?v=CcnLnKU26dg

 

 

 

 

 

 

 

Conversation sur Casus No:

 

Si tu as une vision dialectique (Hegel, entre autres) de l'Histoire humaine, une sinusoïde ne va pas (même "ascendante"), car elle garderait trop de "linéarité" - faisant se succéder des phases ascendantes et descendantes allant quand même de l'avant - tandis qu'en dialectique historique, le moment de la "crise" n'est pas juste un ralentissement ou une baisse, mais une vraie "régression", voire une "négation"- vrai "retour en arrière" ou annulation apparente complète du progrès accompli (c'est le moment où on désespère de l'humanité, qu'on se dit que décidément on n'a rien appris: la guerre, la crise économique, la barbarie "reviennent"!), que le Mouvement de l'Mistoire va cependant devoir "surmonter" et "intégrer", pour une nouveau "progrès" vers la "réalisation de l'esprit" - donc la courbe serait plutôt de cette sorte: une cycloïde trochoïde !

Plus ou moins allongée…





Et je trouve un schéma qui colle assez bien: orienté vers le haut pour illustrer l'optimisme en le Progrès! - et avec des "boucles" qui se touchent pour montrer le "retour" permanent du "passé dans le présent" (le "régressif" étant souvent le "réactionnaire" - engendrant la "révolution" suivante, mais là c'est du Marx).

Ah, et tant que j'y suis! Et si on n'est pas vraiment "zoptimisse" , mais plutôt fataliste, ou "fixiste", donc qu'on refuse la notion de "Progrès", que sans être catastrophiste on a plutôt l'impression que "c'est toujours la même chose de toute façon", que ça ne progresse pas notamment sur le plan moral, que l'humanité se contente de brasser, dans le cercle étroit de son réel, quatre ou cinq obsessions ou idées de base, qui s'imposent un temps, prospèrent, puis dégénèrent ou passent de mode, puis reviennent comme si c'était du neuf, et qu'en fait on n'a rien appris, et pas changé depuis les romains ou la préhistoire? (là on serait plus proche de Nietzsche: une "histoire" vraiment cyclique, à la fois logique et vouée aux crises, mais récurrente, sans échappatoire - sauf individuel peut-être?). Bref, ça tombe bien: je propose alors cette figure d'hypotrochoïde! (jolie animation sur wikipedia)

https://fr.wikipedia.org/wiki/Hypotrocho%C3%AFde

(C'est en gros emprunté à Paul Valery, qui pique l'idée à Nietzsche, et le sociologue Georg Simmel, que j'aime bien, appellait ça, vers 1920 : "la Tragédie de la Culture")

Le cercle bleu, c'est le "champ du possible", le réel quoi; la ligne rouge cycloïde, c'est la pensée humaine.
Quand la ligne rouge sort du cercle bleu, c'est quand la pensée humaine fait une percée dans un domaine, invente une idée, un concept innovant: alors cela devient une création culturelle, qui élargit (en apparence) le domaine du possible: c'est un moment "haut" de l'humanité (genre: Rome, renaissance Italienne, etc… - en fait, tout ce qui laisse une marque culturelle dans l'histoire).
Mais, hélas, tout ce qui a connu un sommet ensuite décline et dégénère: les gens se lassent, ça devient ringard, ou, pire, on se rend compte qu'en fait "ce n'était pas une si bonne idée que ça" (exemples: l'esclavage, l'usage du charbon, etc…). Alors la pensée va dans un "autre sens" à partir du donné, et croit alors inventer "complètement autre chose": c'est une autre pointe de l'étoile (exemple: manger du steak vs devenir vegan).
La "Tragédie" de tout ça, c'est que ça ne va durer qu'un temps, cette nouvelle "mode": on va avoir envie de "revenir en arrière", ou plutôt d'essayer cumuler les deux: c'est la 3ème pointe.
Comme ce sera insatisfaisant (incompatibilité du compromis!) bing, ça repart dans un autre sens (quatrième pointe, selon une logique "réactionnaire"!), mais comme le processus est épuisant, et que la pensée ne peut jamais longtemps se tenir "hors du cercle du réel", finalement on va revenir en gros au point de départ: revival, ou backlash, et surtout re-enfonçage de portes ouvertes: en fait, on "redécouvre la sagesse des anciens", ce genre d'âneries.
Alors oui, pour compliquer, il y a eu parfois un petit décalage, mais pas un "progrès": c'est une boucle, où on sera passés par une série de thèses et d'antithèses, où les mêmes questions se reposent de façon répétitive et cyclique, le tout pour se retrouver en gros pas plus avancés…et toujours "renvoyés au réel" !

 

 

 

Jean Baudrillard, Coool Memories (1980-90), relu:

 

Le problème actuel de la classe politique, c'est qu'il ne s'agit plus de gouverner, mais d'entretenir l'hallucination du pouvoir, ce qui exige des talents très particuliers. Produire le pouvoir comme illusion, c'est comme de jongler avec des capitaux flottants, c'est comme de danser devant un miroir.

Et s'il n'y a plus de pouvoir, c'est que toute la société est passée du côté de la servitude volontaire. Cette mystérieuse figure, sur laquelle on s'est interrogé depuis le XVI^e siècle, n'est plus un mystère désormais, puisqu'elle est devenue la règle générale. Mais d'une façon étrange : non plus comme volonté d'être serf, mais comme chacun devenu serf de sa propre volonté. Sommé de vouloir, de pouvoir, de savoir, d'agir, de réussir, chacun s'est plié à tout cela, et la visée du politique a parfaitement réussi : chacun de nous est devenu un système asservi, auto-asservi, ayant investi toute sa liberté dans la volonté folle de tirer le maximum de lui-même.

 

 

 

 

 

 

 Sur les bias de confirmation, le "bias du survivant":

 

https://fr.wikipedia.org/wiki/Biais_des_survivants?uselang=fr

 

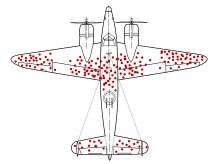
Certain portrayals of disability, such as inspiration porn (where disabled people are able to do ordinary things) and supercrip stereotype (where disabled people do extraordinary things) could be inferred to mean barriers don't exist or that there are no special needs. The media portrayal of successful examples may be cherry picking; many of other people with similar conditions who do not get suitable employment, remain unnoticed. 

https://en.wikipedia.org/wiki/Survivorship_bias#In_studies_of_evolution

 

The push of the past is a type of survivorship bias associated with evolutionary diversification when extinction is possible. Groups that survive a long time are likely to have “got off to a flying start”,and this statistical bias creates an illusion of a true slow-down of diversification rate through time.  

https://en.wikipedia.org/wiki/Push_of_the_past

 

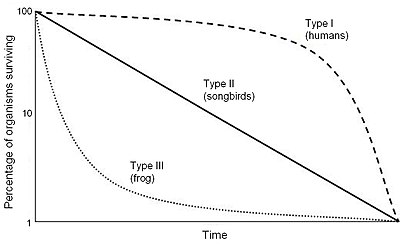
 Courbes de survivabilité:

 

 

 

In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies that the average behavior of the system can be deduced from the trajectory of a "typical" point. Equivalently, a sufficiently large collection of random samples from a process can represent the average statistical properties of the entire process. Ergodicity is a property of the system; it is a statement that the system cannot be reduced or factored into smaller components. Ergodic theory is the study of systems possessing ergodicity.

Ergodic systems occur in a broad range of systems in physics and in geometry. This can be roughly understood to be due to a common phenomenon: the motion of particles, that is, geodesics on a hyperbolic manifold are divergent; when that manifold is compact, that is, of finite size, those orbits return to the same general area, eventually filling the entire space.

Ergodic systems capture the common-sense, every-day notions of randomness, such that smoke might come to fill all of a smoke-filled room, or that a block of metal might eventually come to have the same temperature throughout, or that flips of a fair coin may come up heads and tails half the time. A stronger concept than ergodicity is that of mixing, which aims to mathematically describe the common-sense notions of mixing, such as mixing drinks or mixing cooking ingredients.

The proper mathematical formulation of ergodicity is founded on the formal definitions of measure theory and dynamical systems, and rather specifically on the notion of a measure-preserving dynamical system. The origins of ergodicity lie in statistical physics, where Ludwig Boltzmann formulated the ergodic hypothesis.

The Texas sharpshooter fallacy is an informal fallacy which is committed when differences in data are ignored, but similarities are overemphasized. From this reasoning, a false conclusion is inferred.^[1] This fallacy is the philosophical or rhetorical application of the multiple comparisons problem (in statistics) and apophenia (in cognitive psychology). It is related to the clustering illusion, which is the tendency in human cognition to interpret patterns where none actually exist.

The name comes from a joke about a Texan who fires some gunshots at the side of a barn, then paints a shooting target centered on the tightest cluster of hits and claims to be a sharpshoote

 

Bayesian probability is an interpretation of the concept of probability, in which, instead of frequency or propensity of some phenomenon, probability is interpreted as reasonable expectationrepresenting a state of knowledgeor as quantification of a personal belief.

The Bayesian interpretation of probability can be seen as an extension of propositional logic that enables reasoning with hypotheses;that is, with propositions whose truth or falsity is unknown. In the Bayesian view, a probability is assigned to a hypothesis, whereas under frequentist inference, a hypothesis is typically tested without being assigned a probability.

Bayesian probability belongs to the category of evidential probabilities; to evaluate the probability of a hypothesis, the Bayesian probabilist specifies a prior probability. This, in turn, is then updated to a posterior probability in the light of new, relevant data (evidence).The Bayesian interpretation provides a standard set of procedures and formulae to perform this calculation.

The term Bayesian derives from the 18th-century mathematician and theologian Thomas Bayes, who provided the first mathematical treatment of a non-trivial problem of statistical data analysis using what is now known as Bayesian inference. Mathematician Pierre-Simon Laplace pioneered and popularized what is now called Bayesian probability.

 

The availability heuristic, also known as availability bias, is a mental shortcut that relies on immediate examples that come to a given person's mind when evaluating a specific topic, concept, method or decision. The availability heuristic operates on the notion that if something can be recalled, it must be important, or at least more important than alternative solutions which are not as readily recalled. Subsequently, under the availability heuristic, people tend to heavily weigh their judgments toward more recent information, making new opinions biased toward that latest news.

The availability of consequences associated with an action is positively related to perceptions of the magnitude of the consequences of that action. In other words, the easier it is to recall the consequences of something, the greater those consequences are often perceived to be. Most notably, people often rely on the content of their recall if its implications are not called into question by the difficulty that they experience in bringing the relevant material to mind.^[4]

 

 

 

 

Philippe Sollers:

 « Aux États-Unis, le mot qui revient le plus souvent dans le petit imaginaire des gens qui se racontent des choses sexuelles, c’est le terme « bisexuel » ou encore mieux « androgyne ». Étant donné que le pouvoir féminin là-bas est une réalité palpable, cette croyance à l’androgynie, où vous reconnaissez sans peine le gros succès, définitif peut-être, de Jung, est une chose intéressante. Des femmes, par exemple, croient qu’un transsexuel peut arriver réellement à changer de sexe, exactement comme Schreber pensait que peut-être, en s’enlevant ce petit machin qu’il avait, il deviendrait la femme de Dieu et qu’il réenfanterait l’humanité. On dit qu’il n’y a pas d’idéologie aux États-Unis, mais si, c’est celle-là. » (La notion de mausolée dans le marxisme, décembre 1976. Fugues, folio Gallimard)

 

Pierre legendre:

« Nous assistons aujourd'hui, dans nos sociétés que je qualifie de post-hitlériennes, dans un style autre que le style tyrannique du banditisme hitlérien, cette fois dans la convivialité, l’esprit soi-disant démocratique, la liberté sans frein..., nous assistons au triomphe de l’expérimentation humaine. /…/ je suis étonné qu’on laisse se développer une barbarie qui n’a rien à envier, bien que dans un autre style, à l’esprit du Docteur Mengele. Nous sommes plongés là dedans. Donc, si on parle d’anthropologie, de quoi parlons-nous? On parle aussi, en fait, de quelque chose qui n’a pas de nom et se traduit par la psychotisation des peuples. C’est un problème gravissime. On en a une petite idée avec la barbarie des islamistes fondamentalistes, intégristes... Nous sommes donc dans l’escalade des obscurantismes. L’obscurantisme occidental, qui est un obscurantisme psychotisant, post-hitlérien, trouve aussi sa réponse dans un "je suis encore plus barbare que toi". C’est un cercle infernal qui est ouvert. Et je ne vois pas qu’on fasse autre chose que d’enfermer ces questions dans les nouvelles idéologies universalistes (notamment à base de sexe) ; c’est un combat, et nous verrons où il mène, certainement pas à la démocratie universelle ni à la paix universelle. » (Vues éparses. Entretiens radiophoniques avec Philippe Petit. Editions Mille et une nuits, 2009).

« Aujourd’hui j’ajoute : l’humanité est poussée, du Nord au Sud, à vivre au-dessus de ses moyens psychiques. L’impossibilité de faire admettre ce constat se trouve redoublée à l’occasion de la lutte contre l’épidémie du terrorisme djihadiste : le nécessaire retour sur soi, sur la débâcle généalogique, masquée en Occident par un libertarisme débridé, demeure irrecevable. S’en remettre à l’armée et aux forces de police ne suffira pas, si la réflexion critique est absente. Le refus, par les pédagogues et les instances d’expertises, de changer de cap, c’est-à-dire d’interroger nos propres structures dogmatiques en perdition, met en relief la déroute d’une civilisation devenue incapable de penser l’immémorial universel, la Dette généalogique. » (Sur le site Ars dogmatica, cf. Et cætera)