Sur les bias de confirmation, le "bias du survivant":

 

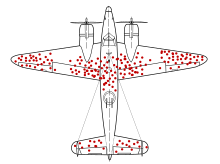
https://fr.wikipedia.org/wiki/Biais_des_survivants?uselang=fr

 

Certain portrayals of disability, such as inspiration porn (where disabled people are able to do ordinary things) and supercrip stereotype (where disabled people do extraordinary things) could be inferred to mean barriers don't exist or that there are no special needs. The media portrayal of successful examples may be cherry picking; many of other people with similar conditions who do not get suitable employment, remain unnoticed. 

https://en.wikipedia.org/wiki/Survivorship_bias#In_studies_of_evolution

 

The push of the past is a type of survivorship bias associated with evolutionary diversification when extinction is possible. Groups that survive a long time are likely to have “got off to a flying start”,and this statistical bias creates an illusion of a true slow-down of diversification rate through time.  

https://en.wikipedia.org/wiki/Push_of_the_past

 

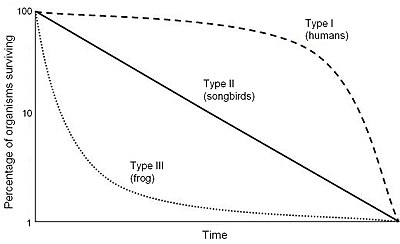
 Courbes de survivabilité:

 

 

 

In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies that the average behavior of the system can be deduced from the trajectory of a "typical" point. Equivalently, a sufficiently large collection of random samples from a process can represent the average statistical properties of the entire process. Ergodicity is a property of the system; it is a statement that the system cannot be reduced or factored into smaller components. Ergodic theory is the study of systems possessing ergodicity.

Ergodic systems occur in a broad range of systems in physics and in geometry. This can be roughly understood to be due to a common phenomenon: the motion of particles, that is, geodesics on a hyperbolic manifold are divergent; when that manifold is compact, that is, of finite size, those orbits return to the same general area, eventually filling the entire space.

Ergodic systems capture the common-sense, every-day notions of randomness, such that smoke might come to fill all of a smoke-filled room, or that a block of metal might eventually come to have the same temperature throughout, or that flips of a fair coin may come up heads and tails half the time. A stronger concept than ergodicity is that of mixing, which aims to mathematically describe the common-sense notions of mixing, such as mixing drinks or mixing cooking ingredients.

The proper mathematical formulation of ergodicity is founded on the formal definitions of measure theory and dynamical systems, and rather specifically on the notion of a measure-preserving dynamical system. The origins of ergodicity lie in statistical physics, where Ludwig Boltzmann formulated the ergodic hypothesis.

The Texas sharpshooter fallacy is an informal fallacy which is committed when differences in data are ignored, but similarities are overemphasized. From this reasoning, a false conclusion is inferred.^[1] This fallacy is the philosophical or rhetorical application of the multiple comparisons problem (in statistics) and apophenia (in cognitive psychology). It is related to the clustering illusion, which is the tendency in human cognition to interpret patterns where none actually exist.

The name comes from a joke about a Texan who fires some gunshots at the side of a barn, then paints a shooting target centered on the tightest cluster of hits and claims to be a sharpshoote

 

Bayesian probability is an interpretation of the concept of probability, in which, instead of frequency or propensity of some phenomenon, probability is interpreted as reasonable expectationrepresenting a state of knowledgeor as quantification of a personal belief.

The Bayesian interpretation of probability can be seen as an extension of propositional logic that enables reasoning with hypotheses;that is, with propositions whose truth or falsity is unknown. In the Bayesian view, a probability is assigned to a hypothesis, whereas under frequentist inference, a hypothesis is typically tested without being assigned a probability.

Bayesian probability belongs to the category of evidential probabilities; to evaluate the probability of a hypothesis, the Bayesian probabilist specifies a prior probability. This, in turn, is then updated to a posterior probability in the light of new, relevant data (evidence).The Bayesian interpretation provides a standard set of procedures and formulae to perform this calculation.

The term Bayesian derives from the 18th-century mathematician and theologian Thomas Bayes, who provided the first mathematical treatment of a non-trivial problem of statistical data analysis using what is now known as Bayesian inference. Mathematician Pierre-Simon Laplace pioneered and popularized what is now called Bayesian probability.

 

The availability heuristic, also known as availability bias, is a mental shortcut that relies on immediate examples that come to a given person's mind when evaluating a specific topic, concept, method or decision. The availability heuristic operates on the notion that if something can be recalled, it must be important, or at least more important than alternative solutions which are not as readily recalled. Subsequently, under the availability heuristic, people tend to heavily weigh their judgments toward more recent information, making new opinions biased toward that latest news.

The availability of consequences associated with an action is positively related to perceptions of the magnitude of the consequences of that action. In other words, the easier it is to recall the consequences of something, the greater those consequences are often perceived to be. Most notably, people often rely on the content of their recall if its implications are not called into question by the difficulty that they experience in bringing the relevant material to mind.^[4]